Eco-evolutionary dynamics of collective function

Mayor evolutionary transitions are marked by the emergence of novel levels of organization, that can result in the coordination of units that were previously independently shaped by natural selection [De Monte & Rainey 2014, Rainey & De Monte 2014]. Despite expectations that competition within heterogeneous cell aggregates should lead to one single, most adapted genotype to dominate in the long term, countless examples in nature witness of the evolutionary stability of mutualistic or symbiotic associations. How can then collective functions that require coexistence of different strains be selected?
We use mathematical models of nested populations, such that birth-death processes occur both for collectives and for their composing particles, to explore how selection acting at the collective level shapes interactions among particle types.
To start, we considered simple collectives composed of two types of particles. Collectives reproduce by dilution at the pace - set by the experimenter - of a collective generation, so that sampling produces offsprings that are in general different from their parent collective. Within collectives, particle types compete with each other, so that frequent dilutions - that keep populations in exponential growth - lead to the fastest type to displace the other. If collectives are given the opportunity to reproduce based on their composition, so that only maximally diverse collectives are passed ot the next collective generation, then it is possible to maintain diversity through the mechanism that was called 'stochastic correction' by Eors Szathmary. Stochastic correction however is a low-yield process, as it relies on sampling to generate a fraction of collective that are sufficiently close to the target composition. Moreover, the collective phenotype (composition) is lost as soon as the selective pressure is discontinued. We showed that when the maximal growth rate and intensity of interactions between types are let evolve, selection for collective function pushes the system towards specific particle-level ecological dynamics, with a mechanism tat we called developmental correction. Such within-collective ecology endows the higher organization level with Darwinian properties, and notably with inheritance of collective-level characters, so that collectives become units of selection in their own right [Doulcier et al. 2019].

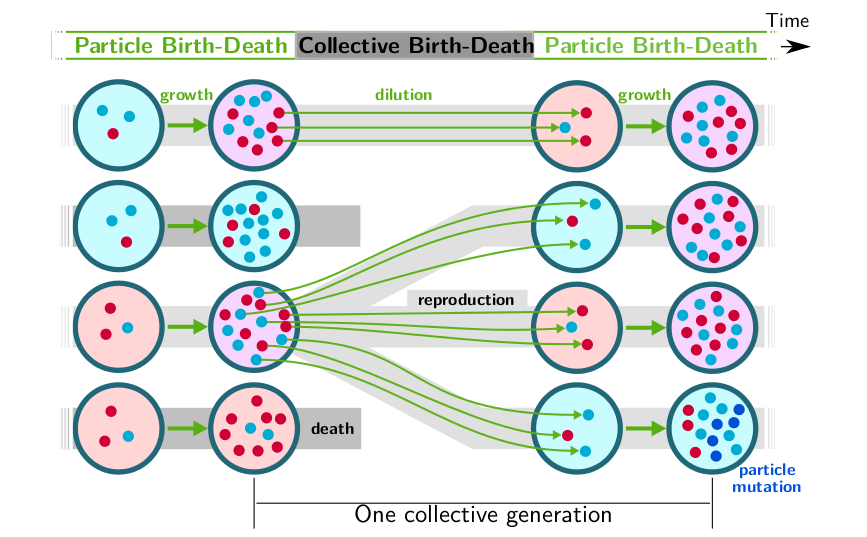
Schematic representation of the nested birth-death processes: the ecological dynamics of particles of different types (red and blue) determines the state of the collective (the fraction of red particles, hence its colour), which affects the death rate of the collectives (pink collectives have higher survival rate).

In collaboration with Giulio Biroli and Jules Fraboul (ENS, Paris), we are currently considering how selection for a collective function (e.g. total biomass) affects the ecological and evolutionary dynamics in communities composed of a large number of species. Generalized Lotka-Volterra equations allow to establish a null model for complex ecosystems, where the strength of interactions among species is assigned at random. By applying methods from statistical physics, we consider the evolution of the macroscopic properties of such communities as the wiring of species interactions changes through 'community-level' mutations. We hope that such analytical insights can complement numerical studies and bring insights onto the best strategies to achieve species coexistence in artificially selected microbial assemblies [De Monte 2021].

Self-organization in aggregative multicellularity

Not only many functions of microbial collectives are achieved by self-organization of phenotypically diverse cells, but the compositional biases created during this process have profound effects on the long-term outcome of repeated interactions. For instance, populations of differentially adhesive particles in an aggregation-dispersion life cycle compensate the costs involved with glue production by biasing group composition [Garcia & De Monte 2016]. A biological system that is particularly adapted for studying the interplay between phenotypic and genetic evolution in self-organization of cellular aggregates is the `social amoeba‘ Dictyostelium discoideum. Its life cycle alternates free-living stages and a multicellular, differentiated, stage. Moreover, chimerae are easily formed mixing not only phenotypically but also genetically diverse sub-populations. Typically, strains that in chimerae produce a higher share of spores are considered social ‘cheaters’ that enhance their reproductive success at the expense of cells who provide the structure of the fruiting body. This perspective directly connects to game theoretical models, that predict that cheaters should doom collective function over evolutionary times. The expectation that cheaters threaten the evolutionary stability of collective structures however essentially depends on the way strategies are conceived [Forget at al. 2020]: do they describe strain- or cell-level behaviour?
We address the cell-level mechanisms that translate initial phenotypic differences among cells (due to either genetic or plastic differences) into spore formation efficiency. In particular, we have considered the evolutionary dynamics of aggregative organisms in populations with heterogeneous adhesion and cell motility. In projects involving Mathieu Forget, Sandrine Adiba (IBENS) and Leonardo Gregory Brunnet (UFRGS, Porto Alegre, Brazil), we study the mechanistic basis of assortment during cell aggregation. This is a key determinant of the predicted outcome of competitive interactions between populations, and thus – on a longer term – of their evolutionary success. We use numerical simulations of self-propelled particles to reproduce experimental observations of frequency-dependent spore biases.
On a more abstract level, we use models coupling ecological and evolutionary dynamics to understand the origin of aggregative life cycles in populations of cells with differential physical properties [Miele & De Monte, 2019]. We consider phenotypes that impacts both individual and collective foraging. For instance, slower cells are disadvantaged in isolation, but can exploit the propulsion by faster cells within multicellular groups (thus behaving as social cheaters). When the level of such exploitation is let evolve, increasing social conflicts are associated to the evolutionary emergence of self-sustained oscillations. Akin to aggregative life cycles, along these life-like cycles resource exhaustion triggers group formation, whereas conflicts within multicellular groups restrain resource consumption, thus paving the way for the subsequent unicellular phase. The evolutionary transition from equilibrium coexistence to life-like cycles solves conflicts among heterogenous cell types by integrating them on a timescale longer than cell division, that comes to be associated to multicellular organization.

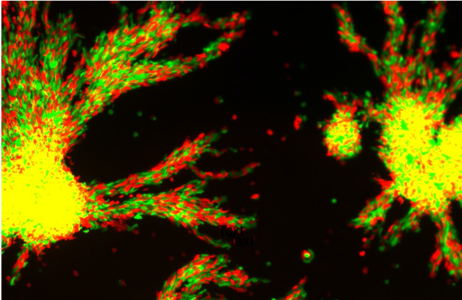
Aggregation of two isogenic Dictyostelium populations harvested at different moments of their demographic cycle.

Abundance distributions in communities

The ecological dynamics of interacting microbial species underpins the abundance of each species in a community. Yet, the relative role of stochastic individual-level birth-death events and of deterministic competition effects in shaping Species Abundance Distributions (SADs) is still unclear. Discriminating what models are most appropriate to describe observations is complicated by the fact that fundamentally different hypotheses provide qualitatively similar predictions. High-throughput methods provide a source of high-resolution data on microbial ecosystems, and allow to go beyond qualitative comparison of theoretical and empirical abundance distributions. We used barcoding abundances for marine plankton protist communities to quantitatively assess SAD variability at the global-scale. We found that plankton communities are composed of two different components, that carry different ecological and geographical information. A small fraction of locally abundant ‘species’ (OTUs) underpins the biogeographical signature of how communities change from one place to another. More than 98% of species are instead found in the `tail‘ of low abundances. These rare sub-communities have a largely conserved abundance distribution, with a power-law decay whose exponent varies less than 10% across the world ocean, and depends only weakly on the organism size [Ser-Giacomi et al. 2018].

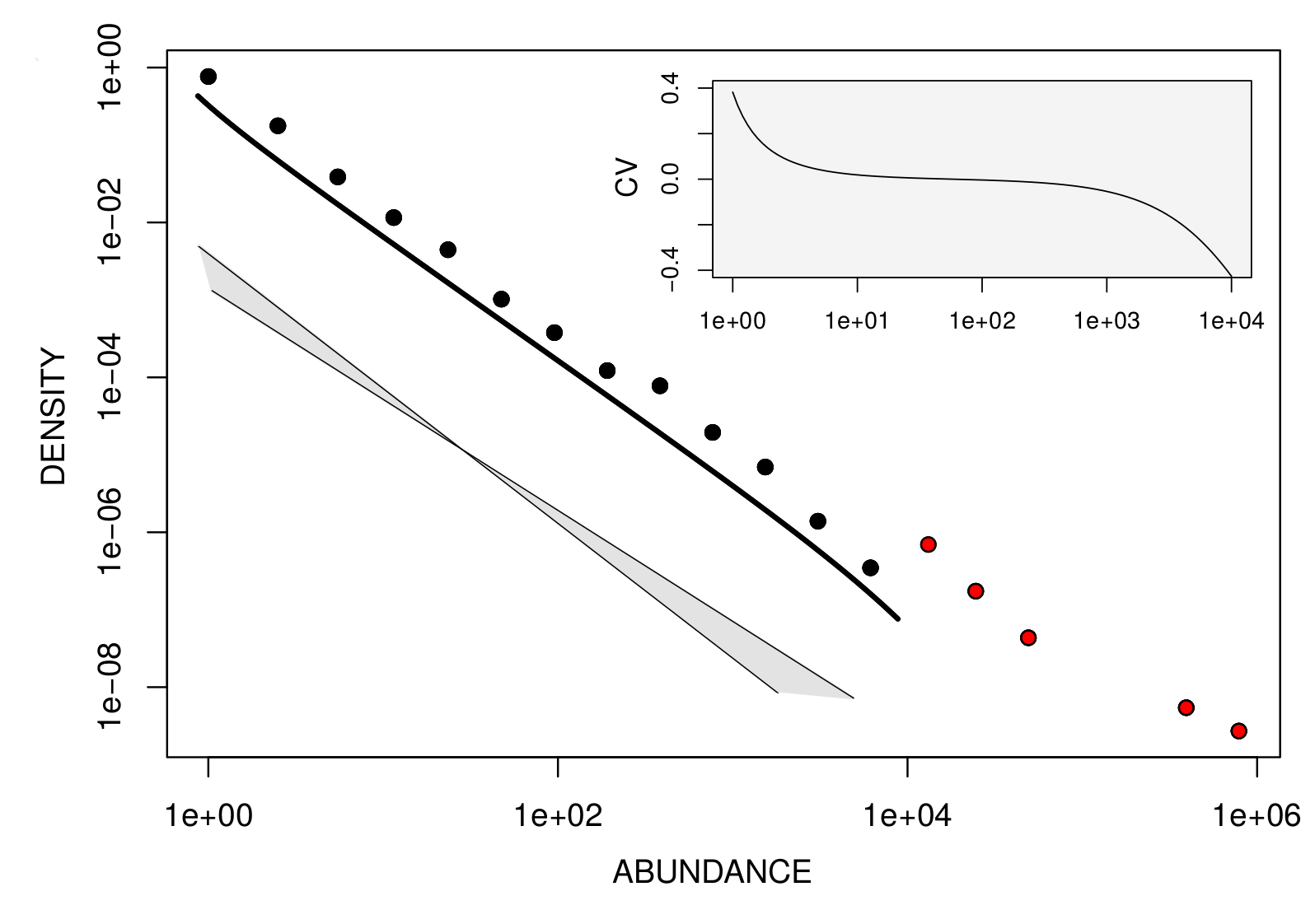
Fitting the distribution of non-dominant planktonic protist species, we found that their decay has small quantitative variations across locations in the global ocean, suggesting that the rare biosphere of planktonic communities is shaped by common ecological processes.

In order to compare distributions quantitatively, we have used a generalization of Hubble‘s neutral model, based on the (quasi-)equivalence of different species in the community. Neutral models are extensively used to generate null hypotheses on the processes underlying community assembly, and have been shown to provide good fits of observed datasets. However, it is not clear what `equivalence in fitness‘ means for planktonic populations that are subjected to intermittency in their environmental forcing and possibly in their ecological dynamics.

Dynamics of complex communities

We explore the dynamics of a class of models where (unlike neutral models) species are assumed to interact with one another, with the aim of understanding how often one should expect the ecological dynamic to be out of equilibrium, how to characterize such regimes and whether it is possible to find effective descriptions applicable to observational data. We use the classic framework of ‘disordered’ Generalized Lotka-Volterra Equations, where species-species interactions α_(i,j) are randomly assigned. Contrary to most models that have been solved by using statistical physics methods, we have focused on the case where interactions – be they competitive or mutualistic – can be strong. Strong interactions imply that, as the number of species in the community increases, the total strength of competition will also increase, making it impossible for many species to coexist simultaneously. If there is no immigration, competitive exclusion eventually results in a cascade of extinctions, so that an equilibrium is reached where species arrange according to a hierarchy of dominance. We realized that, if such extinctions are prevented by immigration, species are abundant or rare only for a limited amount of time, and all species in the community participate in a boom-and-bust turnover that makes ecological dominance unpredictable on the long term, as illustrated in the Figure. Moreover, the properties of the community abundances are mostly captured by those of the single species, which are therefore effectively statistically equivalent. The model predicts a SAD with a broad power-law decay of exponent larger than one, and a one-species approximation suggests applications to observational time series [Mallmin et al. 2024].

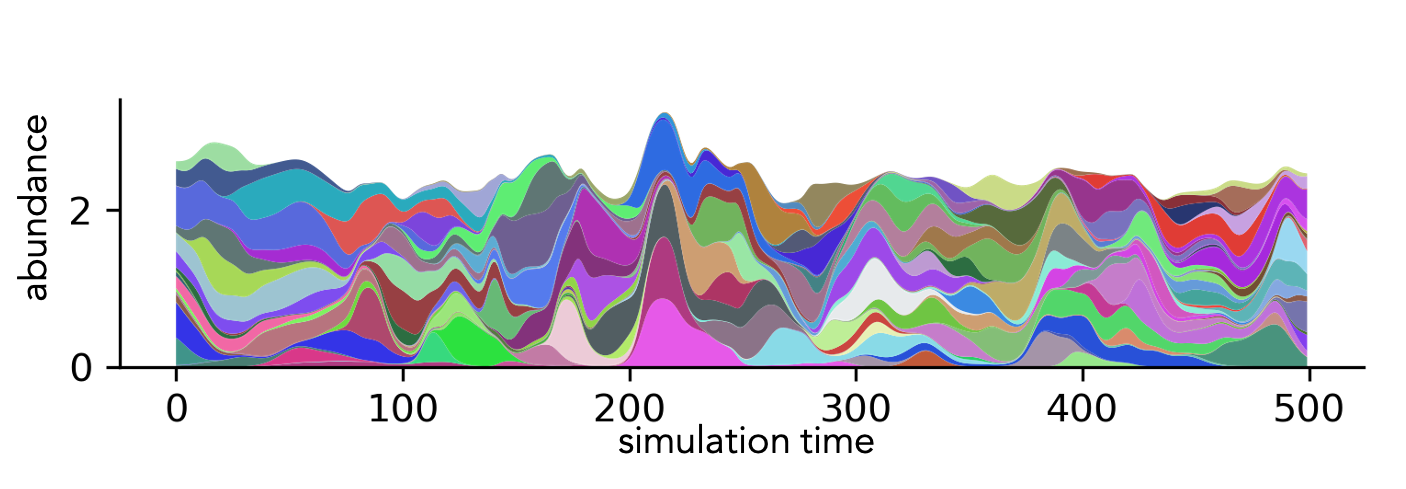
Stacked abundances from a model describing the ecological dynamics of communities with a large number of species that interact strongly with one another.

We are currently expanding these results in two directions: a theoretical exploration of the effect of structure in the interaction network (e.g. due to trophic relations or functional groups), in collaboration with Juan Giral (PhD candidate), Matthieu Barbier, CIRAD, Montpellier and Jeff Arnoldi, CNRS, Montpellier; and the application to empirical time-series, in collaboration with Steve Munch, University of California Santa Cruz, USA.

Evolutionary dynamics and economics

Game theory is a powerful theoretical framework for studying the evolution of cooperative behaviour. I am particularly interested in multi-players games, where the payoff is the result of the simultaneous action of multiple individuals.
In this context, I have studied the role of 'loners' [Hauert et al. 2002], individuals who forego the interaction with others, and instead rely on solitary payoffs that are modest compared to what can be gathered in a group. We have shown that the existence of the option whether to join a public entreprise breaks the classical deadlock between cooperators and cheaters, and leads to non-equilibrium coexistence of all strategies.
In applications to microbes that undergo aggregative life cycles, such as Dictyostelium discoideum, solitary individuals appear as a natural consequence of the process of group formation, whereby any individual has a finite probability of joining in for a collective task. Neither the fact that not all individuals end up cooperating within a group, nor the existence of costs associated to joining (for instance, due the production of an adhesive molecule) preclude the evolution of more and more cohesive groups [Garcia et al. 2015, Garcia & Doulcier et al. 2015].
Although my research currently focuses on microbes, it is unavoidable to wonder to what extent our results may bear implications for human societies. In the other direction, models originally developed for human behaviour have been widely used to interpret observations on microbes, which are sometimes attributed human-like emotions and cognition.
This questioning led me to interact with a group of economists, philosophers of biology and biologists in an exercise of comparison between economics and evolutionary biology. Starting form a list of terms that are central to both disciplines, we discussed the meaning and implications of these terms and how they have been transferred back and forth between fields of investigation [André et al. 2023].